X-MAS CTF 2018 - A white rabbit in a snowstorm
This week, we spritzers played X-MAS CTF 2018. We enjoyed this week-long event, and took the chance to mix things up a bit (e.g., web guys playing pwn). While I’m mainly a pwner, recently I’ve been getting into crypto. I found “A white rabbit in a snowstorm” to be an interesting challenge. It’s probably trivial for the more experienced crypto guys out there, but I had never broken a (very) weakened DES, so I learnt a few things.
If you didn’t know Santa also visits sometime the Hell’s Kitchen! He saw a while ago this beautiful pirece of art, a string called A white rabbit in a snowstorm. But it seems something happend to the string, it got encrypted! Help him decrypt the flag so he can enjoy it’s beauty again!
Here’s the algorithm that was used to encrypt the flag: chall
nc 199.247.6.180 16003
The flag obtained from the challenge must be wrapped up like: X-MAS{flag}
Author: Gabies
I mirrored the algorithm, click on chall in the description to get it.
We’re given a Python script that implements some variation of DES, so let’s have a refresher on DES before continuing.
An overview of DES
The Data Encryption Standard (DES) is a symmetric block cipher, with a key size of 56 bits and a block size of 64 bits. It’s constructed as a balanced Feistel network. Here’s an illustration, courtesy of Wikipedia:
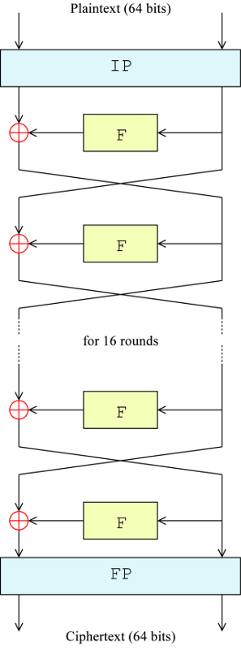
The 64-bit plaintext block is passed through an initial permutation (IP), which reorders the bits, and it is split into two 32-bit halves. Then, the right half becomes the input to a round function (F), and the result is XORed with the left half. The XOR result becomes the right half for the next round, and the right half becomes the next left half. This goes on for 16 rounds, after which the two halves are recombined and treated with a final permutation (FP), which is the inverse of IP, to get the 64-bit ciphertext block. Decryption is exactly the same, but the order of the round subkeys (discussed later) in the round functions is reversed.
Let’s now have a look at the round function (source):
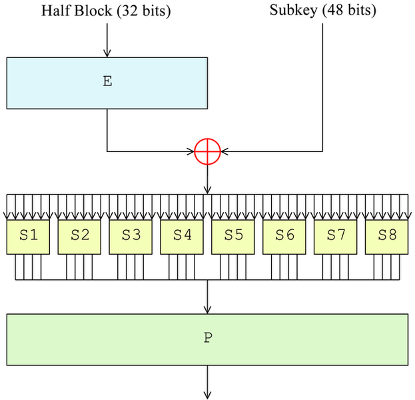
The function takes a 32-bit input and produces a 32-bit output. Each round has a 48-bit subkey, generated in a key schedule before performing encryption/decryption. The input is expanded to 48 bits through an expansion permutation (E), then mixed via XOR with the round subkey. Now comes the crucial part: the mixed result is split into 8 6-bit pieces, which are fed into 8 S-boxes that map 6 input bits to 4 output bits. The S-boxes provide confusion, and in DES they have been carefully selected to hinder cryptanalysis. The 8 4-bit outputs are recombined into a 32-bit word, which is transformed through a permutation P (providing diffusion) to get the final output.
Notice that, if the S-boxes were linear (or affine) functions, then DES would be an affine map. To see why, consider n-bit words as vectors in GF(2)^n. Then unkeyed expansions and permutations are just pre-multiplications by constant matrices, and XOR is addition, so their composition is an affine transformation. The only functions we haven’t considered are the S-boxes, so the non-linearity of the cipher must depend solely on the non-linearity of the S-boxes.
The challenge
When we connect to the challenge, we’re faced with a MD5 proof-of-work to avoid bruteforce/DoS. Once we solve that, we get to the challenge:
Ok, you can continue, go on!
The key will be the same for the encryption and all decryptions during this session!
Here's the encrypted flag: f39b051a98585245!
Here's the partial decription oracle!
Provide a 8-byte string you want to decrypt as hex input:
(the string has to have at least half of the bits different from the ciphertext)
The goal is to decrypt the given block (encrypted flag), and we have a decryption oracle which requires ciphertexts that differ in at least half of the bits from the encrypted flag.
Comparing the challenge’s algorithm with standard DES, we notice that the expansion permutation and the S-boxes have been changed. Specifically, the modified S-boxes map XABCDY to ABCD, i.e., they just drop bits. This is again a linear operation (think of it as a permutation). Actually, there’s an even stronger property: by observing the structure of the expansion function, one quickly realises that S \circ E is the identity function.
By the final argument in the previous section, the whole cipher is an affine map because the S-boxes are linear. Then, in GF(2)^{64}, we can write decryption of the 64x1 bit vector x as G(x) = Ax \oplus b for some 64x64 matrix A and some 64x1 vector b. Intuitively, A represents the permutation components of the cipher, and b represents the XOR components. XORing the ciphertext with some y should produce a simple effect on the plaintext. Let’s check:
\begin{aligned}
G(x \oplus y) &= A(x \oplus y) \oplus b \\
&= Ax \oplus Ay \oplus b \\
&= (Ax \oplus b) \oplus Ay \\
&= G(x) \oplus Ay
\end{aligned}The plaintext is the original plaintext G(x) XORed with Ay. But A is the permutation component, and DES permutations are unkeyed: the key material is only mixed via XOR. Therefore, if we fix y, Ay is constant for any key. We can recover the constant by encrypting (with any key) a known plaintext, XORing the ciphertext with y, decrypting it and XORing the resulting plaintext with the original one.
Now let’s pick y as 0xFFFF…FFFF (64 binary ones). Then XORing with y is equivalent to a bitwise negation. Therefore, the oracle will agree to decrypt the flag ciphertext XORed with y, as all bits are different. We get the plaintext flag XORed with a known constant, so we can recover the original plaintext: Sb0xd3s! (flag is X-MAS{Sb0xd3s!}). The constant was 0xAA…AA (101010… in binary).
Exploit code
#!/usr/bin/env python2
from pwn import *
from hashlib import md5
import string
from des import des # challenge algorithm
XOR_Y = '\xff'*8
xor = lambda x, y: ''.join(chr(ord(a) ^ ord(b)) for a, b in zip(x, y))
d = des()
c = d.encrypt('A'*8, '\x00'*8)
XOR_CONST = d.decrypt('A'*8, xor(c, XOR_Y))
p = remote('199.247.6.180', 16003)
p.recvuntil('md5(X).hexdigest()[:')
n = int(p.recvuntil(']')[:-1])
p.recvuntil('=')
target = p.recvuntil('.')[:-1]
sol = iters.mbruteforce(
lambda x: md5(x).hexdigest()[:n] == target,
string.lowercase, 8)
p.sendline(sol)
p.recvuntil('encrypted flag: ')
flag_enc = p.recvuntil('!')[:-1].decode('hex')
p.recvuntil('ciphertext)\n')
p.sendline(xor(flag_enc, XOR_Y).encode('hex'))
p.recvuntil(' is ')
flag_xor_dec = p.recvuntil('.')[:-1].decode('hex')
flag = xor(flag_xor_dec, XOR_CONST)
print('X-MAS{' + flag + '}')